Portfolio

My research centres on dynamical systems, with a particular focus on Chaos Theory, Bifurcation Theory, and the application of Numerical Methods to vector fields and maps. In 2018, I completed my undergraduate studies as a Mathematical Civil Engineer supervised by Pablo Aguirre at the Universidad Técnica Federico Santa María in Valparaiso, Chile. This formative period cultivated my passion for mathematics and laid the foundation for my doctoral studies. Currently, I am continuing my academic journey in applied mathematics as a PhD student at the University of Auckland, under the supervision of Hinke M. Osinga and Bernd Krauskopf.

I firmly believe in the critical role of dynamical systems in understanding the mysteries of complex phenomena that surround us. Thus, one of my driving motivations is to develop sophisticated numerical methods to not only unravel but also aim to make abstract concepts and complex dynamics accessible through visualisation. I hope to contribute to a broader appreciation and understanding of the mathematical structures that underpin so much of the world around us.

PhD Research

My research centres on a form of chaos called wild chaos. Wild chaos is a new type of dynamics with certain robustness properties that can arise in diffeomorphisms of dimension at least three. The primary objective of my work is to uncover the geometric mechanisms that give rise to this abstract form of chaos in an explicit system.

An essential ingredient in this context is a blender: a geometric object that appears to be higher-dimensional. What does a blender look like? The one-dimensional manifold of a blender ‘looks’ as a surface. As a result of my research, the image shows an example of the destruction of a blender in a three-dimensional Henon-like family as we vary one parameter.

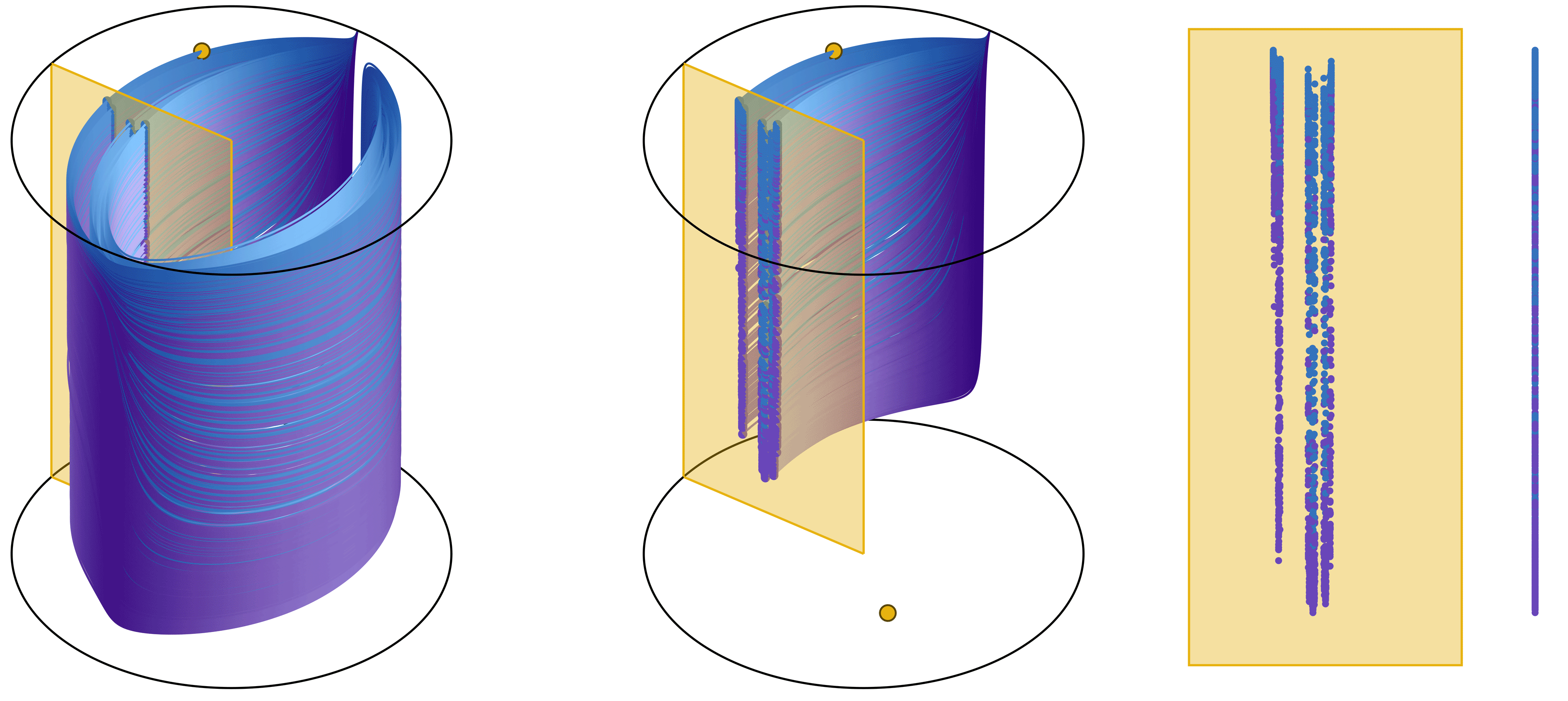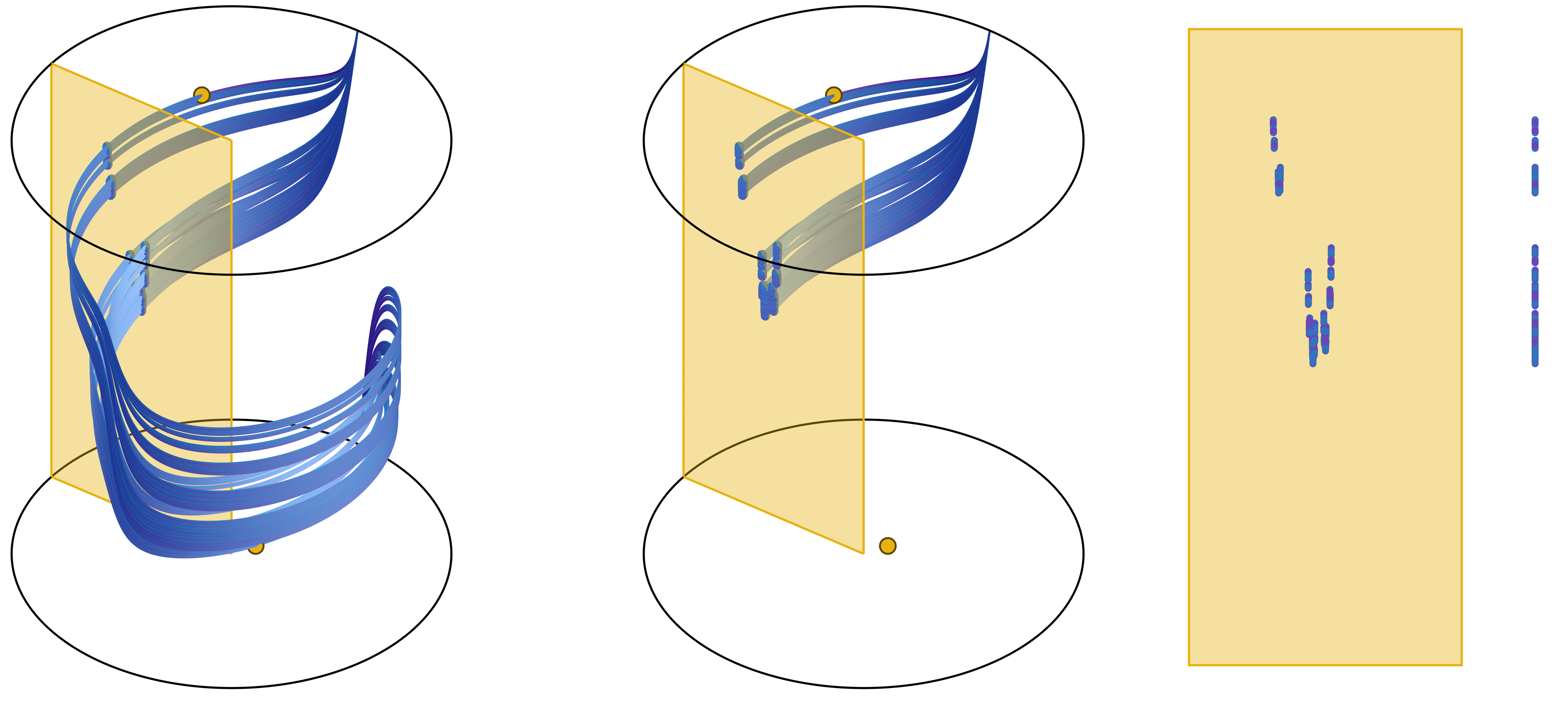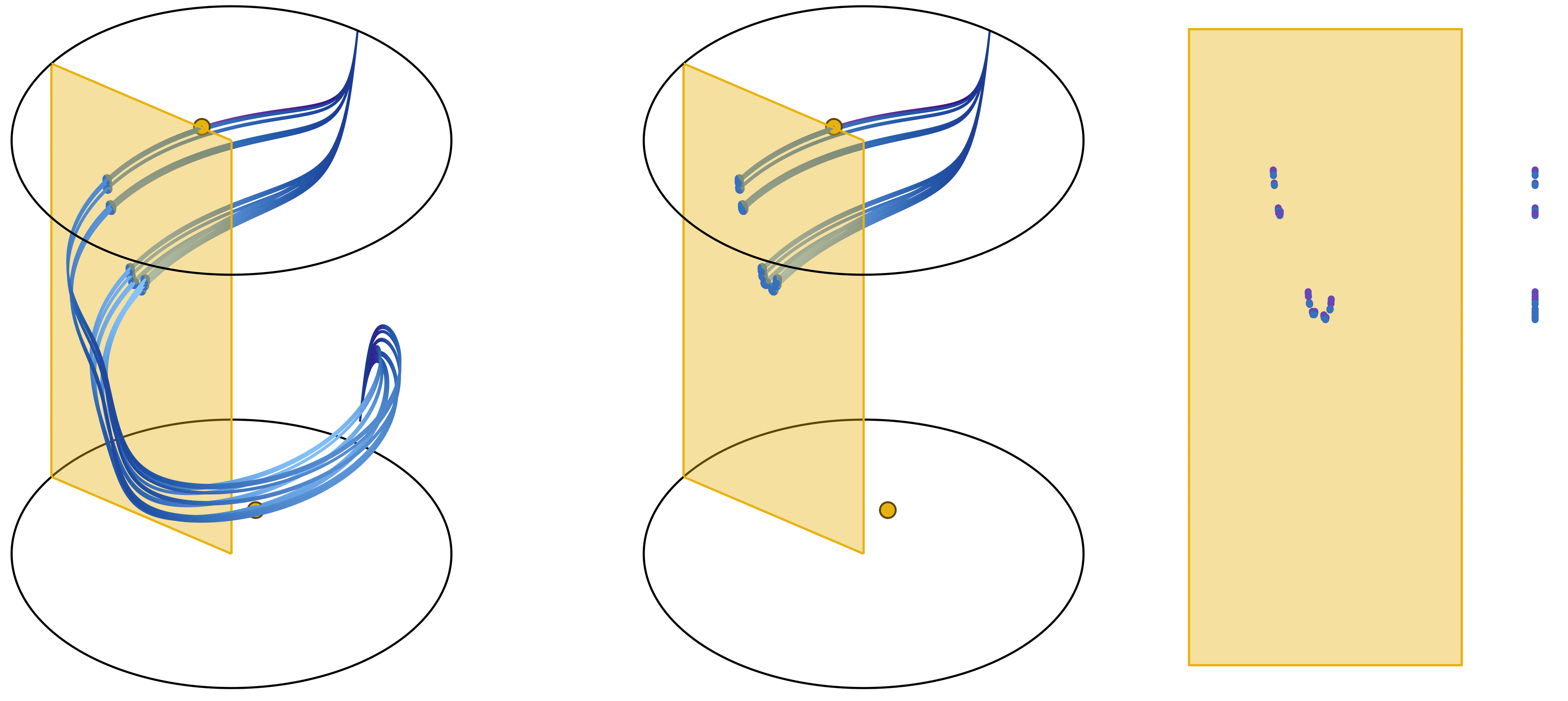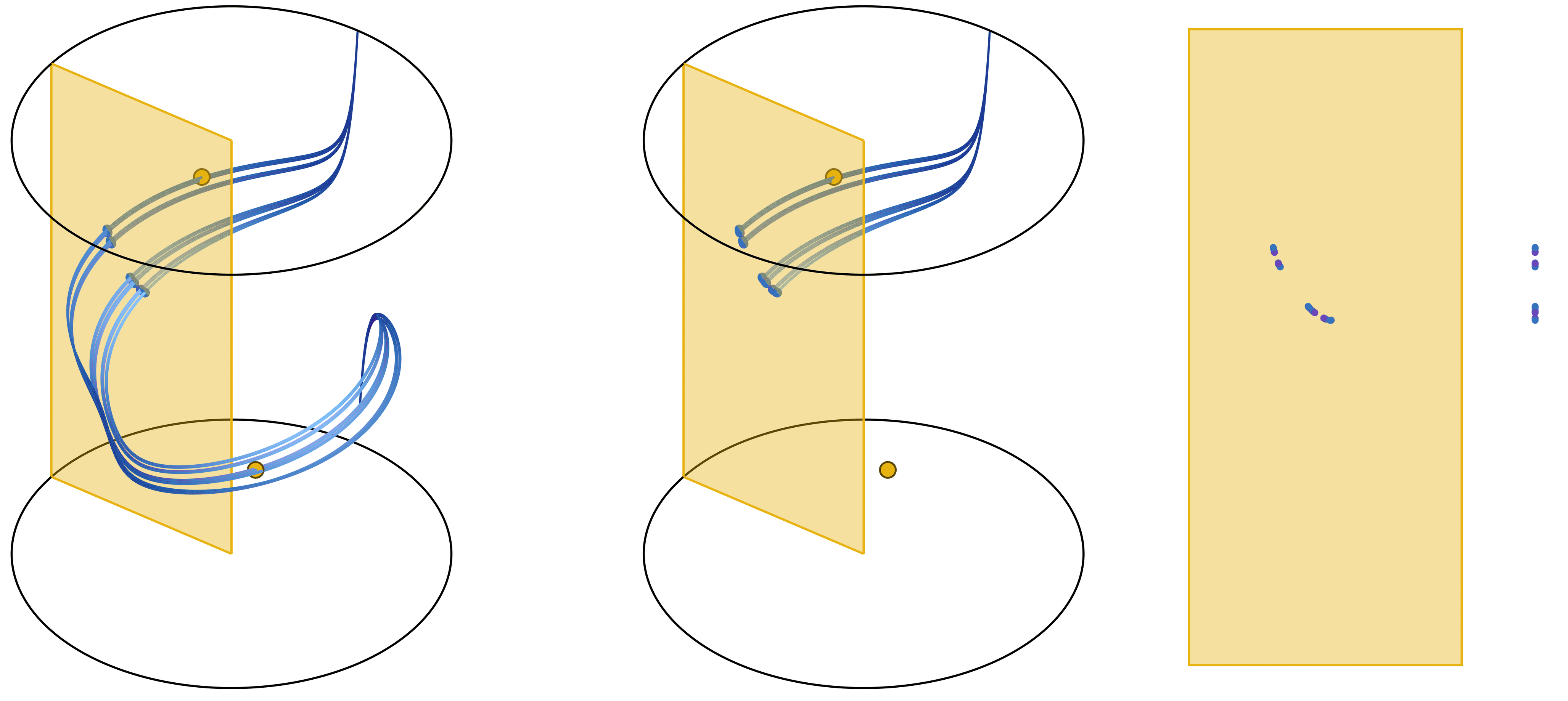
Intersection points of one-dimensional manifolds as a function of xi

The destruction of a blender in a three-dimensional Henon-like family as parameters change. Plotted are the one-dimensional manifolds of two different fixed points and their 2^11 intersection points with a plane.

This was achieved through an algorithm developed in MATLAB to compute the one-dimensional manifolds of a map (preprint and demo available [here]). This approach allows us to topologically characterise the process of a blender’s emergence and shed light on how blenders lose their defining properties as parameters change.

Supervisors: Hinke M. Osinga and Bernd Krauskopf

Publications and Preprints

Computing parametrised large intersection sets of 1D invariant manifolds
Dana C'Julio, Bernd Krauskopf & Hinke M. Osinga,
Preprint
Finding Strategies to Regulate Propagation and Containment of Dengue via Invariant Manifold Analysis
Dana Contreras-Julio, Pablo Aguirre, José Mujica & Olga Vasilieva,
SIAM Journal on Applied Dynamical Systems, 19, pp. 1392-1437, 2020.
Selected for inclusion in SIAM Epidemiology Collection.
Preprint
Allee thresholds and basins of attraction in a predation model with double Allee effect,
Dana Contreras-Julio & Pablo Aguirre,
Mathematical Methods in the Applied Sciences, 41, pp. 2699-2714, 2018.
Preprint

Posters

Blender Hunting: the search for wild chaos (2023)

SGS Research Showcase, University of Auckland, New Zealand.
Awarded the Judges’ Choice Second Place in the Academic Poster category.

Three-dimensional horseshoes and orientation reversal in wild chaos (2021)

SIAM Conference on Applications of Dynamical Systems
Awarded the Red Sock Award for the best poster presentation.

Chaos in the double pendulum (2016)

Festival de las matematicas, Valparaiso, Chile.

Global Dynamics and bifurcations in a predator-prey model with double Allee effect (2015)

XLI Semana de la Matematica, Valparaiso, Chile.
Awarded the best poster presentation.